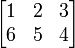Matrizeak Wikipediatik
Matematikan, matrizea zenbakiz osaturiko errenkada (edo zutabe) multzo laukizuzen bat da, beste matrize
batekin batera batu eta biderkatu egin daitekeena. Adibidez, honakoa 2 errenkada eta 3 zutabe dituen matrizea da:
Askotan, matrizeak ekuazio linealetako sistemak planteatu eta ebazteko erabiltzen dira. Halaber, aljebra linealaren
funtsezko tresna dira eta horrela, aplikazio zabalak dituzte zientziaren arlo anitzetan, ekonomiatik (non errenkadaz
errenkada herrialde ezberdinetan izandako gai andana baten ekoizpenak adieraz ditzaketen, esaterako)
fisikara (hiru dimentsiotako kokapenak islatzen denean, adibidez).

matrices wikipedia
sudokus para imprimir
ejemplo : sentido de una matriz
ejemplo : estadística de baloncesto
vitutor : ejercicios de matrices
vadenúmeros: problemas resueltos
Aquí podéis descargaros el archivo con los problemas del bloque A de Selectividad de País Vasco de los últimos años:
PAU País Vasco bloque A : Matrices y programación lineal
Aunque disponemos de geogebra para trabajar con matrices no está de más conocer otras posibilidades:
Exámenes liberatorios resueltos:
- solución liberatorio 1ªeval 2012-13
- solución liberatorio 1ªeval 2013-14
- solución liberatorio 1ªeval 2014-15
- solución liberatorio 1ªeval 2015-16
- solución liberatorio 1ªeval 2016-17
Video : cómo calcular un determinante 3x3
Video : cómo calcular la matriz inversa en matrices 2x2
Video : cómo calcular la matriz inversa en matrices 3x3